基本概念
表达式
- 算术表达式(数值表达式):数学公式
- 逻辑表达式:结果为true或者false
操作符和操作数
一个表达式通常由操作数和操作符组成:
- 操作数:数值或者变量
- 操作符:
- 根据表达式可以分为算术操作符、逻辑操作符
- 根据操作数可以分为单目、双目、三目
中缀表达式、前缀表达式、后缀表达式
操作符存在优先级,例如“先乘除、后加减,如果有括号先计算括号内的表达式”。
传统的中缀表达式对于人来说比较容易理解,但是计算机难以理解,因此诞生了前缀表达式和后缀表达式,只需要按顺序加载计算。
- 中缀表达式(中缀记法):即常见的表达式,运算符在两个操作数中间。例如
(3 + 4) * 5 - 6 - 前缀表达式(波兰式):运算符在操作数之前,按照优先级排好了计算顺序,并且消除了括号。例如
- * + 3 4 5 6 - 后缀表达式(逆波兰式:RPN,Reverse Polish Notation):运算符在操作数之后,按照优先级排好了计算顺序,并且消除了括号。例如
3 4 + 5 * 6 -
这里暂时不考虑阶乘之类的单目符号
表达式计算
public class CalculatorUtil {
private static boolean isOperator(String ch) {
return ch.matches("[+\\-*/]");
}
private static int getPriority(String operator) {
switch (operator) {
case "+":
case "-":
return 1;
case "*":
case "/":
return 2;
}
return -1;
}
private static int calculate(int num1, int num2, String operator) {
switch (operator) {
case "+":
return num2 + num1;
case "-":
return num2 - num1;
case "*":
return num2 * num1;
case "/":
return num2 / num1;
}
return 0;
}
}
先定义几个辅助方法,下面从易到难介绍几种计算方式。
这里暂时不考虑小数点,并且假设参数和表达式合法。
后缀表达式计算
用到一个数栈就够了,只需要遍历表达式,遇到数字直接入栈,遇到符号直接出栈两个数字进行运算,将结果再入栈,直到表达式遍历结束,栈中就剩下一个数字就是计算结果
步骤:使用一个辅助栈,从前往后遍历,遇到操作数直接入栈,遇到运算符,则弹出栈顶两个数字进行运算,并将结果入栈,最后弹出栈顶的数即可。
public class CalculatorUtil {
/**
* 后缀表达式计算
* @param expr 假设按列表拆分,避免遍历拼接数字。
*/
private static int calcSuffix(List<String> expr) {
Stack<Integer> numStack = new Stack<>();
for (int i = 0; i < expr.size(); i++) {
String ch = expr.get(i);
if (isOperator(ch)) {
int num1 = numStack.pop();
int num2 = numStack.pop();
int res = calculate(num1, num2, ch);
numStack.push(res);
} else {
numStack.push(Integer.parseInt(ch));
}
}
return numStack.pop();
}
}
前缀表达式计算
同后缀表达式,不过需要从右往左遍历。
public class CalculatorUtil {
/**
* 前缀表达式计算
* @param expr 假设按列表拆分,避免遍历拼接数字。
*/
private static int calcPrefix(List<String> expr) {
Stack<Integer> numStack = new Stack<>();
//前缀表达式从右往左遍历
for (int i = expr.size() - 1; i >= 0; i--) {
String ch = expr.get(i);
if (isOperator(ch)) {
int num1 = numStack.pop();
int num2 = numStack.pop();
//注意:这里num1和num2要交换一下
int res = calculate(num2, num1, ch);
numStack.push(res);
} else {
numStack.push(Integer.parseInt(ch));
}
}
return numStack.pop();
}
}
相比之下,后缀表达式实现起来更容易,且便于理解,所以一般采用中缀转后缀计算。另外一个好处是,中缀转后缀的过程中,可以边转换边计算。
例如我们平常写表达式的代码,编译器和解释器基本都是转为后缀表达式进行计算。
中缀表达式计算
步骤:
- 初始化两个栈,一个是符号栈s1,一个是操作数栈s2
- 从左到右扫描中缀表达式
- 遇到操作数直接入栈s2,需要遍历拼接数字
- 遇到运算符时,比较其与栈顶运算符的优先级
- 当栈为空,或者栈顶为左括号时,则将运算符入栈s1
- 当优先级大于栈顶运算符时,将运算符入栈s1
- 当优先级小于等于栈顶运算符时,就弹出栈顶运算符和两个操作数进行计算,并将计算结果压入数栈s2,直到栈为空或当前运算符优先级大于栈顶运算符优先级,将当前运算符加入符号栈s1。
- 遇到括号时
- 如果是左括号,直接入栈s1;
- 如果是右括号,依次弹出s1中的运算符和两个操作数进行计算,并将计算结果压入数栈s2,直到遇见左括号为止,此时将一对括号丢弃。
- 直到整个表达式遍历结束,再将s1中剩余的运算符依次弹出,和两个操作数进行计算,并将计算结果压入数栈s2。直到符号栈为空,此时栈顶的数字就是表达式的计算结果。
public class CalculatorUtil {
private static int calcInfix(String expr) {
final Stack<Integer> numStack = new Stack<>();
final Stack<String> operatorStack = new Stack<>();
for (int i = 0; i < expr.length(); i++) {
//全部转换为String进行处理,避免用char判断ASCII编码
String ch = String.valueOf(expr.charAt(i));
if ("(".equals(ch)) {
operatorStack.push(ch);
} else if (")".equals(ch)) {
while (!operatorStack.isEmpty()) {
String operator = operatorStack.pop();
if ("(".equals(operator)) {
break;
}
int num1 = numStack.pop();
int num2 = numStack.pop();
int res = calculate(num1, num2, operator);
numStack.push(res);
}
} else if (isOperator(ch)) {
while (!operatorStack.isEmpty() && getPriority(ch) <= getPriority(operatorStack.peek())) {
int num1 = numStack.pop();
int num2 = numStack.pop();
String operator = operatorStack.pop();
int res = calculate(num1, num2, operator);
//计算中间结果,压入操作数栈
numStack.push(res);
}
operatorStack.push(ch);
} else {
//遍历拼接数字
StringBuilder numStr =new StringBuilder();
int j = i;
while (j < expr.length() && Character.isDigit(expr.charAt(j))) {
numStr.append(expr.charAt(j));
j++;
}
i = j - 1;
int num = Integer.parseInt(numStr.toString());
numStack.push(num);
}
}
//弹出剩余的符号进行计算
while (!operatorStack.isEmpty()) {
int num1 = numStack.pop();
int num2 = numStack.pop();
String operator = operatorStack.pop();
int res = calculate(num1, num2, operator);
numStack.push(res);
}
return numStack.pop();
}
}
中缀表达式转后缀表达式
步骤:
- 初始化两个栈,一个是符号栈s1,一个是结果栈s2
- 从左到右扫描中缀表达式
- 遇到操作数直接入栈s2
- 遇到运算符时,比较其与栈顶运算符的优先级
- 当栈为空,或者栈顶为左括号时,则将运算符入栈s1
- 当优先级大于栈顶运算符时,将运算符入栈s1
- 当优先级小于等于栈顶运算符时,就弹出栈顶运算符压入s2,直到栈为空或当前运算符优先级大于栈顶运算符优先级,将当前运算符压入栈s1
- 遇到括号时
- 如果是左括号,直接入栈s1;
- 如果是右括号,依次弹出s1中的运算符压入s2,直到遇见左括号为止,此时将一对括号丢弃
- 直到整个表达式遍历结束,再将s1中剩余的运算符依次弹出压入s2
- 此时将s2中元素依次弹出,再逆序即为后缀表达式。(可以使用队列简化,依次弹出队头元素)
过程和中缀表达式计算类似,只是不需要计算中间结果,而是将操作符直接加入结果栈中。并且最后需要逆序输出。
public class CalculatorUtil {
/**
* 中缀表达式转后缀表达式
*/
public static String infixToSuffix(String expr) {
//由于最后需要逆序输出栈内元素,可以简化为使用队列
Deque<String> res = new LinkedList<>();
Stack<String> operatorStack = new Stack<>();
for (int i = 0; i < expr.length(); i++) {
String ch = String.valueOf(expr.charAt(i));
if ("(".equals(ch)) {
operatorStack.push(ch);
} else if (")".equals(ch)) {
while (!operatorStack.isEmpty()) {
String operator = operatorStack.pop();
if (operator.equals("(")) {
break;
}
res.push(operator);
}
} else if (isOperator(ch)) {
while (!operatorStack.isEmpty() && getPriority(ch) <= getPriority(operatorStack.peek())) {
String operator = operatorStack.pop();
//直接将运算符压入结果栈
res.push(operator);
}
operatorStack.push(ch);
} else {
StringBuilder numStr = new StringBuilder();
int j = i;
while (j < expr.length() && Character.isDigit(expr.charAt(j))) {
numStr.append(expr.charAt(j));
j++;
}
i = j - 1;
res.push(numStr.toString());
}
}
while (!operatorStack.isEmpty()) {
String operator = operatorStack.pop();
res.push(operator);
}
StringBuilder sb = new StringBuilder();
while (!res.isEmpty()) {
sb.append(res.pollLast());
}
return sb.toString();
}
}
边界情况
上面的案例中没有处理边界情况和异常情况等,例如
- 表达式中第一个数为负数,此时
-只有单目,少了一个操作数:可以在表达式开头补0,或者提前将0压入操作数栈 - 括号内的第一个数为负数:需要将
(-替换为(0- - 小数点后面没有数字的话要补0,例如3.==>3.0,或者判断非法
- 忽略所有空格
中缀表达式转二叉树
步骤:
- 找到优先级最低的操作符,作为根结点,运算符两边的表达式分别为左右子树
- 继续拆分左右子树
- 最终叶子结点一定是操作数,根节点是操作符
- 此时二叉树前序遍历即前缀表达式,后序遍历即后缀表达式
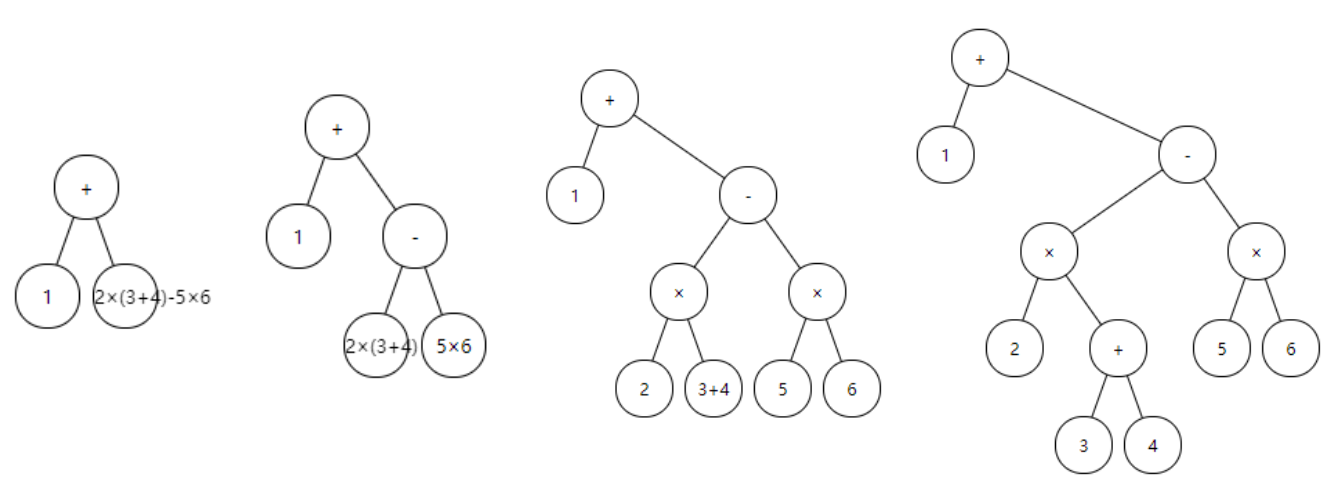
以1 + 2 ∗ (3 + 4) − 5 * 6为例
先拆分+,如图
- 前缀表达式:
[+, 1, -, *, 2, +, 3, 4, *, 5, 6] - 后缀表达式:
[1, 2, 3, 4, +, *, 5, 6, *, -, +]
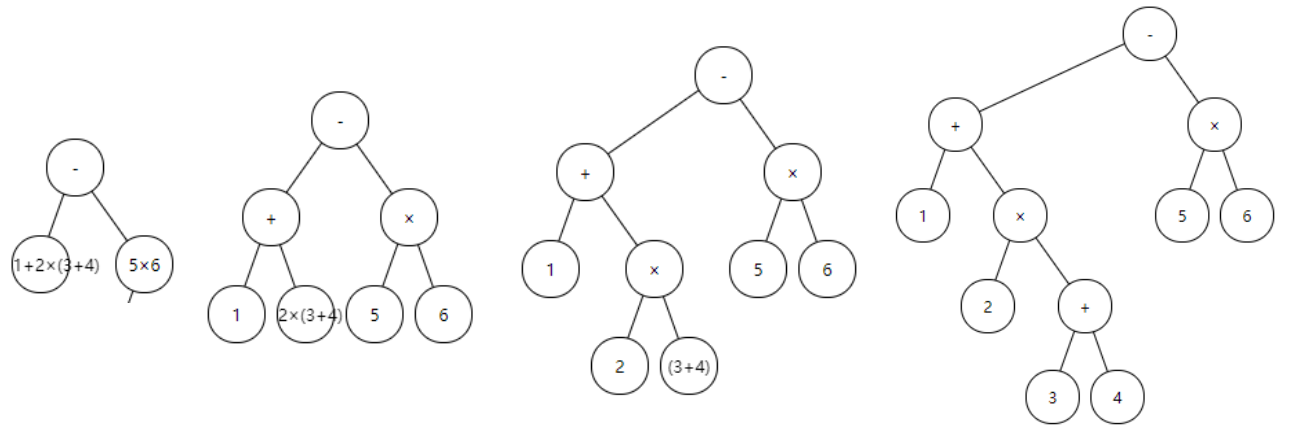
先拆分-,如图
- 前缀表达式:
[-, +, 1, *, 2, +, 3, 4, *, 5, 6] - 后缀表达式:
[1, 2, 3, 4, +, *, +, 5, 6, *, -]
通过上一节的代码计算出结果均为15,可以看出"两个操作符优先级相同时,先拆分哪一个都行"
建议先拆分靠后的运算符,作为根节点:按照上一节"中缀转后缀"的计算方式,靠后的运算符会被放到栈顶,最后逆序输出,因此最后的运算符是根节点。
public class CalculatorUtil {
public static void main(String[] args) {
System.out.println("calcInfix: (1+2*(3+4)-5*6) = " + calcInfix("1+2*(3+4)-5*6"));
System.out.println("infixToSuffix: (1+2*(3+4)-5*6) = " + infixToSuffix("1+2*(3+4)-5*6"));
System.out.println("calcSuffix: (1 2 3 4 + * 5 6 * - +) = " + calcSuffix(Arrays.asList("1 2 3 4 + * 5 6 * - +".split(" "))));
System.out.println("calcPrefix: (- + 1 * 2 + 3 4 * 5 6) = " + calcPrefix(Arrays.asList("- + 1 * 2 + 3 4 * 5 6".split(" "))));
System.out.println("calcSuffix: (1 2 3 4 + * + 5 6 * -) = " + calcSuffix(Arrays.asList("1 2 3 4 + * + 5 6 * -".split(" "))));
System.out.println("calcPrefix: (+ 1 - * 2 + 3 4 * 5 6) = " + calcPrefix(Arrays.asList("+ 1 - * 2 + 3 4 * 5 6".split(" "))));
}
}
计算器APP
开发计算器APP时,可以限制输入,防止出现非法表达式,梳理了部分限制逻辑
+、*、/不能在开头或者是(后- 不能有两个连续运算符,连续输入两次运算符要覆盖掉前一个
(只能在运算符和(之后。)只能在操作数或者)之后,且数量不超过()后面不能是数字- 一个操作数不能有两个小数点
. - 小数点后要接数字
- 操作数为0,后面不能再加0
- 全部退格之后,空字符串显示0
- 不合法表达式按
=无响应 - 操作符前后可以加空格,避免遍历查找操作数,例如(12+34)==>( 12 + 34 ),计算的时候可以直接按空格分割